Shopping for term life insurance

Posted on January 16, 2013 by Siddharth Jain

Ideally we want a policy with variable payoff:
payoff = P(1-\frac{x}{T})(1+r)^x
where,
P = payoff you want if you die today
T = an appropriate length of time (not necessarily the term of the insurance; see the example of 20yr policy in the article)
r = rate of inflation e.g., 0.03
x = time when payoff occurs
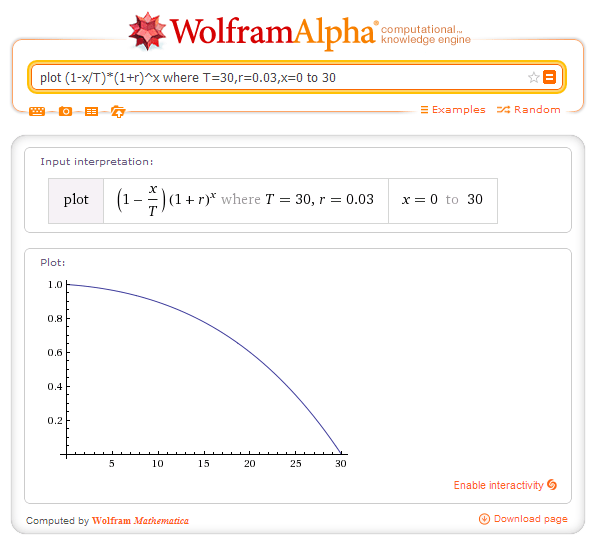
plot1

Since such policies are not available, we will do averaging over the term of the policy to obtain mean value, and use that as the coverage we want. To do this, we need to compute the integral:
figure2

For 20 year policy:
figure3
Average would be 17.29/20 = 0.86.

For 30 year policy:
figure4
Average would be 20/30 = 0.67.

One way to approximate the variable payoff is to buy 3 policies:

  • A 10 year term policy with cover equal to e_1
  • A 20 year term policy with cover equal to e_2
  • A 30 year term policy with cover equal to e_3

Then, the payoff e would be as follows:
e = \begin{array}{rcl} e_1 + e_2 + e_3 & \mbox{for} & x \in [0,10] \\ e_2 + e_3 & \mbox{for} & x \in (10,20] \\ e_3 & \mbox{for} & x \in (20,30] \\ \end{array}
We want:
e_1 + e_2 + e_3 = \frac{1}{10}\int_0^{10}P \left(1-\frac{x}{30}\right)*1.03^xdx = 0.96P

e_2 + e_3 = \frac{1}{10}\int_{10}^{20} P\left(1-\frac{x}{30}\right)*1.03^xdx = 0.769P

e_3 = \frac{1}{10}\int_{20}^{30} P\left(1-\frac{x}{30}\right)*1.03^xdx = 0.333P

which gives:
e_1 = 0.191P, e_2 = 0.436P, e_3 = 0.333P
Of course, in practice you have to compare total of premiums for the 3 policies vs. premium total for a single policy in order to justify buying 3 policies. As an example with P = $581,000, and using quotes from http://www.term4sale.com:
Option1: buying 1 policy. 30 yr term with coverage = 20.62/30*$581,000 = $400,000 costs $30/mo
Option2: buying 3 policies
e_1 = $111,150 which needs to be rounded to $100,000. premium for this is $7.66/mo
e_2 = $253,730 which needs to be rounded to $250,000. premium for this is $13.27/mo
e_3 = $193.786 which needs to be rounded to $200,000. premium for this is $20.6/mo
Let us also incorporate inflation. Total of premiums inflation adjusted for Option1 =

\int_0^{30} \frac{30}{1.03^t}dt = 596.79

For Option2 we get:

\int_0^{10} \frac{41.53}{1.03^t}dt + \int_{10}^{20} \frac{33.87}{1.03^t}dt + \int_{20}^{30} \frac{20.6}{1.03^t}dt
= 359.547 + 218.191 + 98.7453 = 676.48

So buying 3 policies is more expensive, but then that’s the price you pay to get variable payoff.

Bonus: calculating maxima (highest payoff) using wolfram alpha:
maxima

Qs to ask:

  • can premium change? don’t buy policies where premium can change.
  • is policy cancellable? don’t buy non-cancellable policies.
  • what happens if I move to another country?
  • what are the criteria for qualifying for preferred plus coverage?
This entry was posted in Money. Bookmark the permalink.

Leave a comment